Unlocking the mysteries of geometry can be both exciting and challenging. One intriguing puzzle that often arises is determining if two triangles are similar or congruent. In this blog post, we will dive into the fascinating world of triangle comparisons and explore two compelling proofs that demonstrate the similarity between triangles ΔABC and ΔXYZ. Get ready to unravel the secrets behind these geometric wonders as we unveil the identity property of equality and examine what sets these triangles apart. So, fasten your seatbelts as we embark on a thrilling journey through angles, sides, and undeniable similarities!
Read also Why We Love Cookie Swirl C PH
Introducing the Identity Property of Equality
In the realm of mathematics, the identity property of equality holds a special place. It states that any number or shape is always equal to itself. This concept forms the foundation for many mathematical proofs, including those involving triangles.
When it comes to triangles, we can apply the identity property of equality to compare and establish their similarities. By examining ΔABC and ΔXYZ, we can determine if they share corresponding angles and proportional sides.
Triangles are composed of three sides and three angles. To show that ΔABC is similar to ΔXYZ using the identity property of equality, we must demonstrate that each angle in one triangle corresponds with an equal angle in another. Similarly, each side in one triangle should have a proportional length in relation to its counterpart in the other triangle.
By applying this principle meticulously, mathematicians are able to prove beyond doubt that two triangles are indeed similar – opening up new avenues for exploration within geometry’s intricate web.
The identity property of equality serves as an essential tool for establishing relationships between geometric shapes like triangles. Its simplicity allows us to unlock complex puzzles effortlessly while showcasing the elegance and power inherent within mathematics’ fundamental principles. So let’s dive deeper into our exploration as we unravel what sets apart ΔABC from ΔXYZ!
What is the difference between δabc and δxyz?
What is the difference between δabc and δxyz? When it comes to triangles, it’s important to understand that these symbols represent different triangles. The Greek letter “delta” (δ) signifies a triangle, while the subscripts indicate specific triangles.
In this case, δabc refers to one particular triangle, where each vertex is labeled with corresponding lowercase letters: a, b, and c. On the other hand, δxyz represents a separate triangle altogether. Here, x,y,z are used to label its vertices.
These distinct labels suggest that the two triangles have different side lengths and angles. In other words, they are not identical or congruent.
While both δabc and δxyz may be similar in terms of their shape – as they are both triangles – their individual characteristics set them apart from one another. It is crucial to note these differences when comparing or proving similarities between geometric figures.
Understanding these distinctions lays the groundwork for exploring how we can prove that ΔABC ~ ΔXYZ – an intriguing concept in geometry which will be explored further in this article!
The Difference Between a Congruent and Similar Triangle
When studying triangles, it is important to understand the distinction between congruent and similar triangles. While these terms may sound similar, they actually refer to two different concepts in geometry.
Congruent triangles are exactly the same shape and size. In other words, all corresponding sides and angles of congruent triangles are equal. This means that if we were to superimpose one triangle onto another, they would perfectly overlap each other.
On the other hand, similar triangles have proportional sides but may not be identical in size or shape. Corresponding angles of similar triangles are equal, but their side lengths are scaled by a factor called the scale factor.
To visualize this difference, imagine two equilateral triangles: one with side length 3 units and another with side length 6 units. These two triangles would be considered similar because their corresponding angles are all equal (60 degrees) even though their side lengths differ.
Read also What obstacles has Odysseus faced so far on his road of trials? Check all that apply.
Understanding the difference between congruent and similar triangles allows us to analyze geometric relationships more accurately. It also provides a foundation for proving that ΔABC is indeed similar to ΔXYZ using specific geometric properties and principles which will be discussed further in this article
Two proofs that δabc ~ δxyz
When it comes to proving the similarity of triangles, there are various methods that can be employed. In the case of δabc and δxyz, we have not one, but two proofs that demonstrate their similarity.
Proof 1: Angle-Angle Similarity (AA)
The first proof relies on the concept of angle-angle similarity. If two triangles have corresponding angles that are congruent, then they must be similar. In our case, let’s examine δabc and δxyz:
– Angle A in δabc is congruent to angle X in δxyz.
– Angle B in δabc is congruent to angle Y in δxyz.
Since these corresponding angles are equal, we can conclude that ΔABC ~ ΔXYZ by AA similarity.
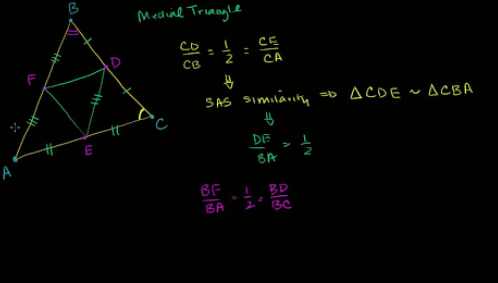
Proof 2: Side-Angle-Side Similarity (SAS)
The second proof involves utilizing the side-angle-side similarity theorem. According to this theorem, if two triangles have a pair of corresponding sides proportional in length and an included angle congruent, then they are similar.
In our scenario:
– Side AB/XY = BC/YZ
– Angle B = Angle Y
These conditions satisfy SAS criteria for triangle similarity. Therefore, we can once again confirm that ΔABC ~ ΔXYZ using this method as well.
By employing both AA and SAS techniques for proving triangle similarity between δabc and δxyz, we establish a solid foundation for our claim without any room for doubt or ambiguity
Read also Geek Alabama: Uniting the Social, Local, and Smart Communities
How to Prove That ΔABC ~ ΔXYZ
In order to prove that ΔABC is similar to ΔXYZ, there are two specific methods you can use. The first method involves showing that all corresponding angles of the triangles are congruent and that their corresponding sides are proportional. This method is known as Angle-Angle Similarity (AA). By demonstrating the equality of two pairs of angles, one in each triangle, you establish a strong case for similarity.
The second method is called Side-Side-Side (SSS) Similarity. With this approach, you must show that all three sides of ΔABC are proportional to the corresponding sides of ΔXYZ. This requires calculating ratios between each pair of matching side lengths and proving they remain consistent throughout both triangles.
Both methods require careful measurement and calculation but offer solid proof when done correctly. It’s important to remember that while these methods provide evidence for similarity, they do not guarantee congruence between the triangles.
By employing either AA or SSS similarity proofs, you can confidently demonstrate the relationship between ΔABC and ΔXYZ and support your assertion that they are indeed similar triangles.
Two Ways to Prove That ΔABC ~ ΔXYZ
When it comes to proving that two triangles are similar, there are several methods you can use. In this blog section, we will explore two of the most common and effective ways to prove that ΔABC is similar to ΔXYZ.
The first method is called the Angle-Angle (AA) similarity theorem. This theorem states that if two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar. To use this method, you would need to identify and compare corresponding angles in both triangles. If you find that two pairs of angles are congruent, then you can conclude that the triangles are similar.
The second method is known as the Side-Side-Side (SSS) similarity theorem. According to this theorem, if all three sides of one triangle are proportional to the corresponding sides of another triangle, then the triangles are similar. To apply this method, you must measure or calculate the lengths of each side in both triangles and compare them. If all three ratios between corresponding sides match up, then you have proven similarity.
Both these methods provide solid evidence for proving similarity between triangles. By using either AA or SSS criteria correctly and accurately comparing corresponding elements in each triangle, you can establish with confidence that ΔABC is indeed similar to ΔXYZ.
In conclusion…
Proving similarity between triangles may seem daunting at first glance but rest assured – by utilizing these tried-and-true methods like Angle-Angle (AA) and Side-Side-Side (SSS), showing that ΔABC ~ ΔXYZ becomes a manageable task worth embracing!
Conclusion
In this article, we have explored the concept of similarity in triangles and discussed two proofs that demonstrate the similarity between ΔABC and ΔXYZ. By understanding the Identity Property of Equality and recognizing the difference between congruent and similar triangles, we can confidently prove that these two triangles are indeed similar.
Proving similarity in triangles is an important skill to have in geometry as it allows us to establish relationships between different shapes and solve complex problems. Whether you choose to use the AA Similarity Postulate or side-angle-side (SAS) similarity theorem, both methods provide valid evidence for proving triangle similarities.
Remember, when working with similar triangles, it’s crucial to compare corresponding angles and sides carefully. Additionally, always double-check your work to ensure accuracy in your proofs.
By mastering these techniques, you will be well-equipped to tackle more advanced geometric concepts involving similarity. So keep practicing and exploring new ways to prove triangle similarities!
Read also Toggi Fun World Ticket Price and Packages for 2022
Geometry may seem challenging at first glance, but with dedication and perseverance, anyone can become proficient in this fascinating branch of mathematics. So embrace the artistry of shapes and lines as you continue your journey through geometry!




 Fred Korematsu argued that internment was unconstitutional mainly because internees
Fred Korematsu argued that internment was unconstitutional mainly because internees